
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.
Zobacz więcej:
- dla uczniów szkół podstawowych: oij.edu.pl/start/
- dla uczniów szkół średnich: oi.edu.pl/l/jak_zaczac/
Zadanie Pochylnia (poc)
Pomóż nam usprawnić bazę zadań!
Pochylnia
Limit pamięci: 32 MB
Na pochylni na nabrzeżu portowym są ułożone w przypadkowej kolejności beczki w trzech kolorach: czerwone, zielone i niebieskie. Trzeba je uporządkować, za pomocą dźwigu w taki sposób, aby na początku (najniżej) były czerwone, następnie niebieskie, a na końcu (najwyżej) zielone.
Dźwig - w jednym ruchu - może podnieść do góry jednocześnie trzy sąsiednie beczki w dowolnym miejscu na pochylni i przenieść je na koniec, za beczki leżące powyżej, które stoczą się pod własnym ciężarem w dół wypełniając lukę.
Trzeba ułożyć plan pracy dźwigu dyktujący w kolejnych ruchach, którą trójkę beczek przenieść na koniec.
Ułożenie beczek na pochylni zapisujemy za pomocą ciągu  liter
liter
 ,
,  ,
,  , gdzie
, gdzie  to liczba beczek.
Litery
to liczba beczek.
Litery  ,
,  ,
,  w tym ciągu symbolizują
odpowiednio beczkę czerwoną, niebieską lub zieloną. Zakładamy, że liczba beczek
w tym ciągu symbolizują
odpowiednio beczkę czerwoną, niebieską lub zieloną. Zakładamy, że liczba beczek
 jest nie większa niż
jest nie większa niż  oraz, że na pochylni są
przynajmniej
oraz, że na pochylni są
przynajmniej  beczki zielone.
beczki zielone.
Plan porządkowania beczek za pomocą dźwigu można zapisać w postaci skończonego
ciągu 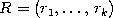 liczb całkowitych dodatnich nie
większych niż
liczb całkowitych dodatnich nie
większych niż  . Kolejny
. Kolejny  -ty wyraz ciągu
-ty wyraz ciągu  to pozycja (licząc od dołu) najniższej z trzech beczek, jakie należy
przenieść na koniec w
to pozycja (licząc od dołu) najniższej z trzech beczek, jakie należy
przenieść na koniec w  -tym ruchu.
-tym ruchu.
Przykład
9 beczek ułożonych na pochylni w kolejności: (czerwona, zielona, niebieska,
niebieska, czerwona, niebieska, zielona, zielona, niebieska) zapisujemy za
pomocą ciągu:  .
.
Dźwig pracujący według planu  będzie zmieniał ich
ułożenie w następujący sposób:
będzie zmieniał ich
ułożenie w następujący sposób:  ,
,  ,
,
 i po trzech
ruchach uporządkuje je w kolejności czerwone-niebieskie-zielone.
i po trzech
ruchach uporządkuje je w kolejności czerwone-niebieskie-zielone.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia liczbę beczek
 , a następnie
ciąg
, a następnie
ciąg  liter
liter  ,
,  ,
,  określający
początkowe ułożenie beczek na pochylni,
określający
początkowe ułożenie beczek na pochylni, - układa plan porządkowania beczek w kolejności czerwone-niebieskie-zielone w postaci odpowiedniego skończonego ciągu liczb całkowitych dodatnich i zapisuje ten plan na standardowym wyjściu.
Dla każdego ułożenia początkowego beczek (jeśli są przynajmniej trzy beczki zielone) istnieje wiele planów ich porządkowania w kolejności czerwone-niebieskie-zielone. Mogą się one różnić liczbą ruchów. Twój program powinien znaleźć i wypisać tylko jeden z nich. Liczba ruchów nie musi być minimalna, aby rozwiązanie było poprawne. Powinieneś jednak dążyć do tego by Twój program układał plany porządkowania beczek w możliwie małej liczbie ruchów i aby znajdował je możliwie jak najszybciej.
Wejście
- W pierwszym wierszu standardowego wejścia jest zapisana jedna liczba
całkowita
 nie mniejsza niż
nie mniejsza niż  i nie większa niż
i nie większa niż
 . Jest to liczba beczek na pochylni.
. Jest to liczba beczek na pochylni. - W każdym z kolejnych
 wierszy jest zapisany jeden znak - litera
wierszy jest zapisany jeden znak - litera
 ,
,  albo
albo  , określająca kolor odpowiedniej
kolejnej beczki na pochylni. W tym ciągu
, określająca kolor odpowiedniej
kolejnej beczki na pochylni. W tym ciągu  znaków są przynajmniej 3
litery
znaków są przynajmniej 3
litery  .
.
Wyjście
- Na standardowym wyjściu należy zapisać odpowiedni skończony ciąg liczb całkowitych dodatnich, który jest planem porządkowania ułożenia beczek.
- Każdą liczbę tego ciągu należy zapisać w osobnym wierszu.
Przykład
Dla danych wejściowych:
9 c z n n c n z z n
poprawną odpowiedzią jest:
6 2 5
Autor zadania: Andrzej Walat.

 English
English